Sparse singular vectors¶

The left singular vectors associated with the smallest and largest singular values of a matrix \(A\) (globally) minimize and maximize \(\|Ax\|_2\) subject to \(\|x\|_2 = 1\).

(We could also limit a nonconvex sparsifier, as above in sparse recovery.)

This leads to the problems

where \(x \in \mathbb{R}^n\) is the variable and \(\mu \geq 0\) controls the sparsification, to find \(x\) that is sparse, satisfies \(\|x\|_2 = 1\), and makes \(\|Ax\|_2\) small or large.

We call such a vector, with some abuse of notation, a sparse singular vector.

Since \(\|x\|_2 = 1\), we know \(1 \leq \|x\|_1 \leq \sqrt{n}\), so the range of \(\mu\) can be set as \([1, \sqrt{n}]\).

[1]:

import matplotlib.pyplot as plt
import numpy as np
import cvxpy as cp
from dccp import is_dccp

rng = np.random.default_rng(seed=0)
m = 10
n = 10
A0 = np.random.randn(m, n)
U, Sigma, V = np.linalg.svd(A0, full_matrices=False)
Sigma = Sigma / Sigma[-1]
A = np.dot(U, np.dot(np.diag(Sigma), V))

# smallest singular value
mu = cp.Parameter(nonneg=True)
x = cp.Variable(n)
cost = cp.norm(A @ x)
constr = [cp.norm(x, 2) == 1, cp.norm(x, 1) <= mu]
obj = cp.Minimize(cost)
prob = cp.Problem(obj, constr)
singular_value = []
card = []
x_result = []
mu_vals = np.linspace(1, np.sqrt(n), 50)

for val in mu_vals:
    mu.value = val
    prob.solve(method="dccp", max_iter=50)
    assert is_dccp(prob)
    singular_value.append(cp.norm(A @ x).value)
    card.append(np.sum(np.abs(x.value) >= 1e-2))
    x_result.append(x.value)

Numerical example¶

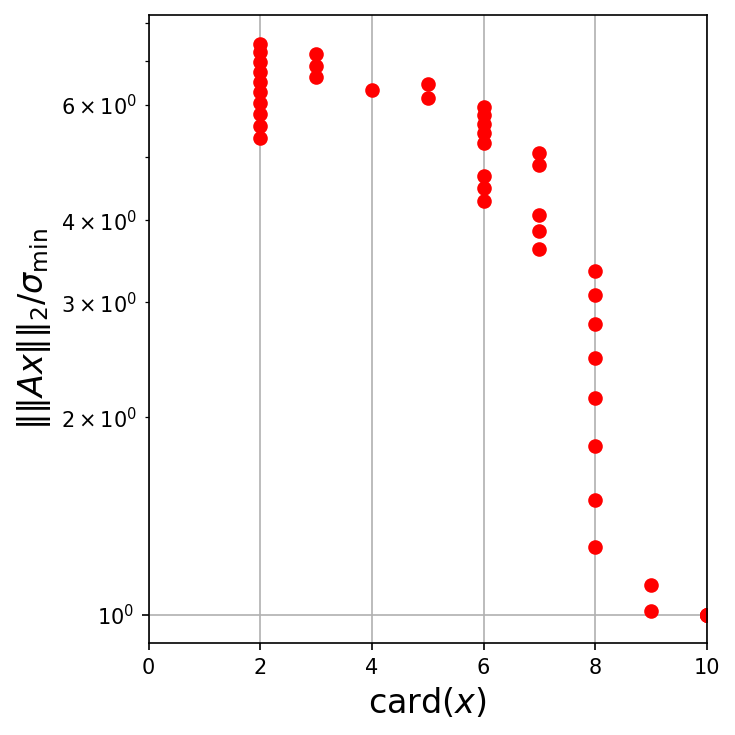
We consider an instance for minimization with a random matrix \(A \in \mathbb{R}^{100 \times 100}\) with i.i.d. entries \(A_{ij} \sim \mathcal{N}(0,1)\), with (positive) smallest singular value \(\sigma_{\min}\).

The parameter \(\mu\) is swept from 1 to 10 with increment 0.2, and for each value of \(\mu\) the result of solving the problem above is shown as a red dot.

The most left point in the figure corresponds to \(\|x\|_1 \leq 1\), which gives cardinality 1.

In this instance it achieves the globally optimal value, which is the smallest of the norm of the columns of \(A\).

[2]:

plt.figure(figsize=(5, 5), dpi=150)
for ind in range(len(card)):
    plt.plot(card[ind], singular_value[ind], "r o")
plt.xlim([0, n])
plt.yscale("log")
plt.grid()
plt.ylabel(r"$\|\|Ax\|\|_2/\sigma_{\mathrm{min}}$", fontsize=16)
plt.xlabel("card($x$)", fontsize=16)
plt.tight_layout()