Path planning¶
The goal is to find the shortest path connecting points \(a\) and \(b\) in \(\mathbb{R}^d\) that avoids \(m\) circles, centered at \(p_j\) with radius \(r_j\), \(j = 1, \ldots, m\).
After discretizing the arc length parametrized path into points \(x_0, \ldots, x_n\), the problem is posed as
\[\begin{split}\begin{array}{ll}
\text{minimize} & L \\
\text{subject to} & x_0 = a, \quad x_n = b, \\
& \|x_i - x_{i-1}\|_2 \leq L/n, \quad i = 1, \ldots, n, \\
& \|x_i - p_j\|_2 \geq r_j, \quad i = 1, \ldots, n, \; j = 1, \ldots,
m,
\end{array}\end{split}\]
where \(L\) and \(x_i\) are variables, and \(a, b, p_j\), and \(r_j\) are given.
[1]:
import cvxpy as cp
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
import numpy as np
from dccp import is_dccp
n = 50
l = 10
m = 5
a = np.array([0, 0]).T
b = np.array([l, l]).T
d = 2
p = np.array([[2, 4.5, 6, 7, 8.5], [2.2, 5, 8, 6, 9]])
r = [1, 0.8, 0.4, 1.4, 0.5]
x = []
for i in range(n + 1):
x += [cp.Variable((d, 1))]
L = cp.Variable(1)
constr = [x[0] == a, x[n] == b]
cost = L
for i in range(n):
constr += [cp.norm(x[i] - x[i + 1]) <= L / n]
for j in range(m):
p_j = p[:, j:j+1] # Keep 2D shape by using slice notation
constr += [cp.norm(x[i] - p_j) >= r[j]]
prob = cp.Problem(cp.Minimize(cost), constr)
assert is_dccp(prob)
result = prob.solve(method="dccp")
assert prob.status == cp.OPTIMAL, "DCCP failed to find optimal solution"
assert result is not None, "DCCP failed to find a solution"
/home/langestefan/dev/cvx/dccp/.venv/lib64/python3.13/site-packages/cvxpy/reductions/solvers/solving_chain_utils.py:30: UserWarning: The problem includes expressions that don't support CPP backend. Defaulting to the SCIPY backend for canonicalization.
warnings.warn(UserWarning(
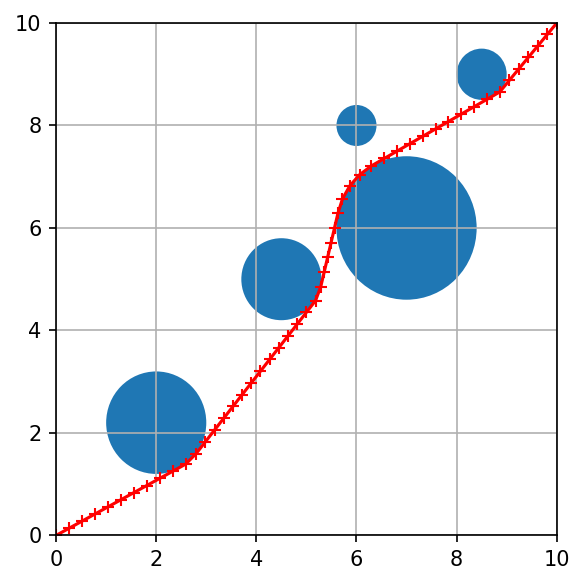
Visualization of the trajectory¶
To visually validate the solution we plot the optimal trajectory and ensure it avoids the circular obstacles.
[2]:
fig, ax = plt.subplots(figsize=(4, 4))
for i in range(m):
center = tuple(p[:, i])
circle = mpatches.Circle(center, r[i], ec="none")
ax.add_patch(circle)
ax1 = [xx.value[0] for xx in x]
ax2 = [xx.value[1] for xx in x]
plt.plot(ax1, ax2, "r-+")
plt.ylim(0, 10)
plt.xlim(0, 10)
ax.grid()
fig.set_dpi(150)
fig.tight_layout()