Phase retrieval¶
Phase retrieval is the problem of recovering a signal \(x_0 \in \mathbb{C}^n\) from the magnitudes of the complex inner products \(x_0^* a_k\), for \(k = 1, \ldots, m\), where \(a_k \in \mathbb{C}^n\) are the given measurement vectors.
The recovery problem can be expressed as
\[\begin{split}\begin{array}{ll}
\text{find} & x \\
\text{subject to} & |x^* a_k| = y_k, \quad k = 1, \ldots, m,
\end{array}\end{split}\]
where \(x \in \mathbb{C}^n\) is the optimization variable, and \(a_k\) and \(y_k \in \mathbb{R}_+\) are given. The lefthand side of the constraints are convex quadratic functions of the real and imaginary parts of the arguments, which are in turn linear functions of the variable \(x\).
Model definition¶
The following code segment specifies the problem.
DCCP does not yet support complex variables and constants, so we expand complex numbers into real and imaginary parts.
[1]:
"""DCCP package."""
import cvxpy as cp
import matplotlib.pyplot as plt
import numpy as np
from dccp import is_dccp
# Set up random number generator for reproducibility
rng = np.random.default_rng(42)
n = 128
m = 3 * n
# data
x0r = rng.random((n, 1))
x0i = rng.random((n, 1))
Ar = rng.random((m, n))
Ai = rng.random((m, n))
yr = np.dot(Ar, x0r) + np.dot(Ai, x0i)
yi = np.dot(Ar, x0i) - np.dot(Ai, x0r)
y = np.power(yr, 2) + np.power(yi, 2)
y = np.power(y, 0.5)
# problem definition
xr = cp.Variable((n, 1))
xi = cp.Variable((n, 1))
x = cp.Variable((2, n))
z = []
constr = []
c = np.array([[0, 1], [-1, 0]])
for k in range(m):
z.append(cp.Variable((2, 1)))
z[-1].value = -rng.random((2, 1))
constr.append(cp.norm(z[-1]) == y[k])
constr += [
z[-1] == x @ np.reshape(Ar[k, :], (n, 1)) + c @ x @ np.reshape(Ai[k, :], (n, 1))
]
# solve the problem
prob = cp.Problem(cp.Minimize(0), constr)
assert is_dccp(prob)
result = prob.solve(method="dccp", seed=0)
assert prob.status == cp.OPTIMAL
assert result is not None
Visualize the results¶
[2]:
fig, (ax0, ax1) = plt.subplots(nrows=2, figsize=(10, 8), dpi=150)
tan = np.array(x[0, :].value / x[1, :].value)
angle = np.arctan(tan)
tan0 = x0r / x0i
angle0 = np.arctan(tan0)
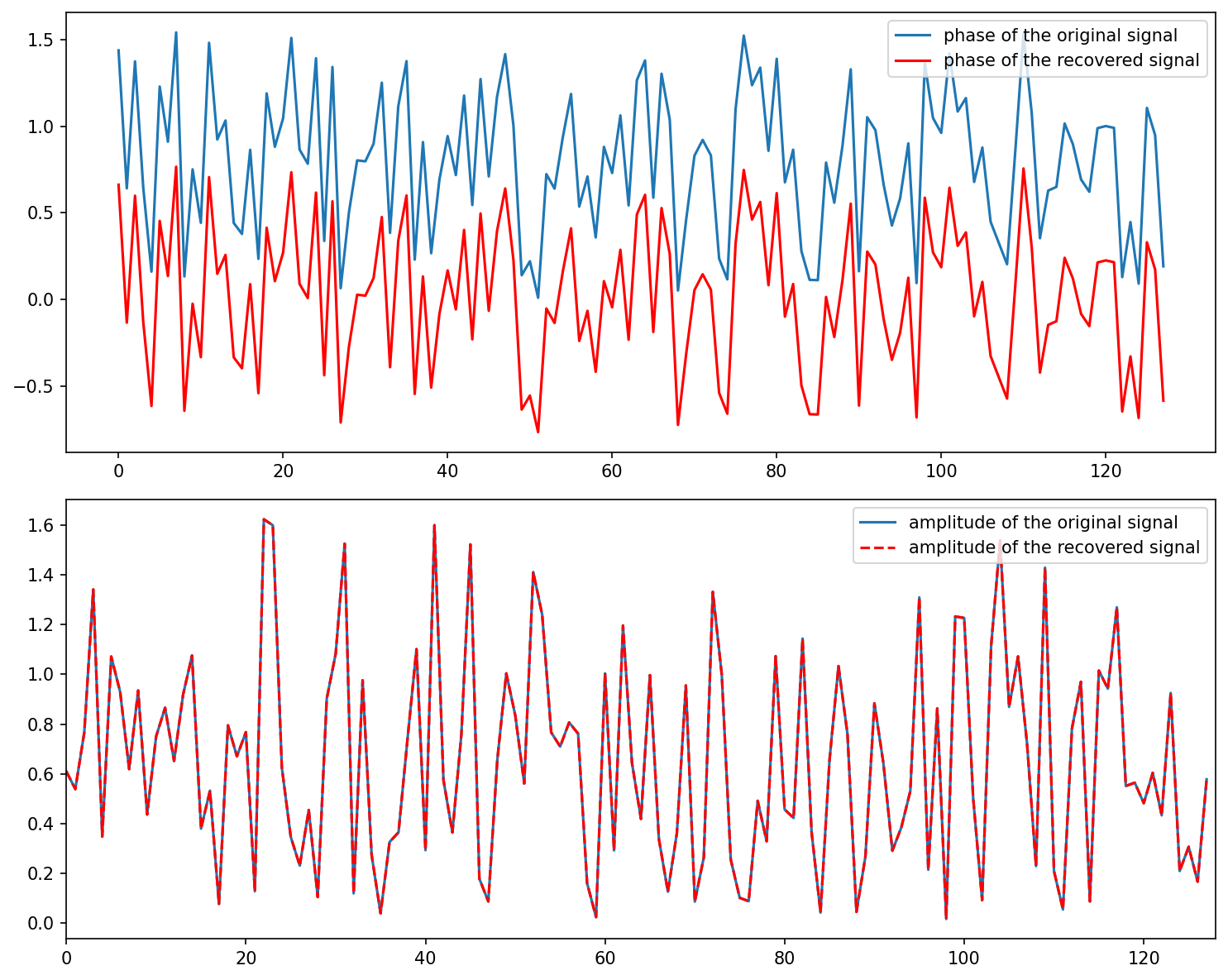
ax0.plot(angle0)
ax0.plot(angle, "r")
plt.xlim([0, 128])
ax0.legend(["phase of the original signal", "phase of the recovered signal"])
ax1.plot(np.array(np.power(x0r, 2) + np.power(x0i, 2)))
ax1.plot(np.array(np.power(x[0, :].value, 2) + np.power(x[1, :].value, 2)), "r--")
plt.xlim([0, 128])
ax1.legend(["amplitude of the original signal", "amplitude of the recovered signal"])
plt.tight_layout()