Lagged and Iterated Differences

The lagged and iterated differences of a vector. If x is length n, this function returns a length \(n-k\) vector of the \(k\)th order difference between the lagged terms. diff(x) returns the vector of differences between adjacent elements in the vector, i.e. [x[2] - x[1], x[3] - x[2], ...]. diff(x,1,2) is the second-order differences vector, equivalently diff(diff(x)). diff(x,1,0) returns the vector x unchanged. diff(x,2) returns the vector of differences [x[3] - x[1], x[4] - x[2], ...], equivalent to x[(1+lag):n] - x[1:(n-lag)].

# S4 method for Expression
diff(x, lag = 1, differences = 1, ...)

Arguments

x

An Expression.

lag

An integer indicating which lag to use.

differences

An integer indicating the order of the difference.

...

(Optional) Addition axis argument, specifying the dimension across which to apply the function: 1 indicates rows, 2 indicates columns, and NA indicates rows and columns. The default is axis = 1.

Value

An Expression representing the kth order difference.

Examples

## Problem data
m <- 101
L <- 2
h <- L/(m-1)

## Form objective and constraints
x <- Variable(m)
y <- Variable(m)
obj <- sum(y)
constr <- list(x[1] == 0, y[1] == 1, x[m] == 1, y[m] == 1, diff(x)^2 + diff(y)^2 <= h^2)

## Solve the catenary problem
prob <- Problem(Minimize(obj), constr)
result <- solve(prob)

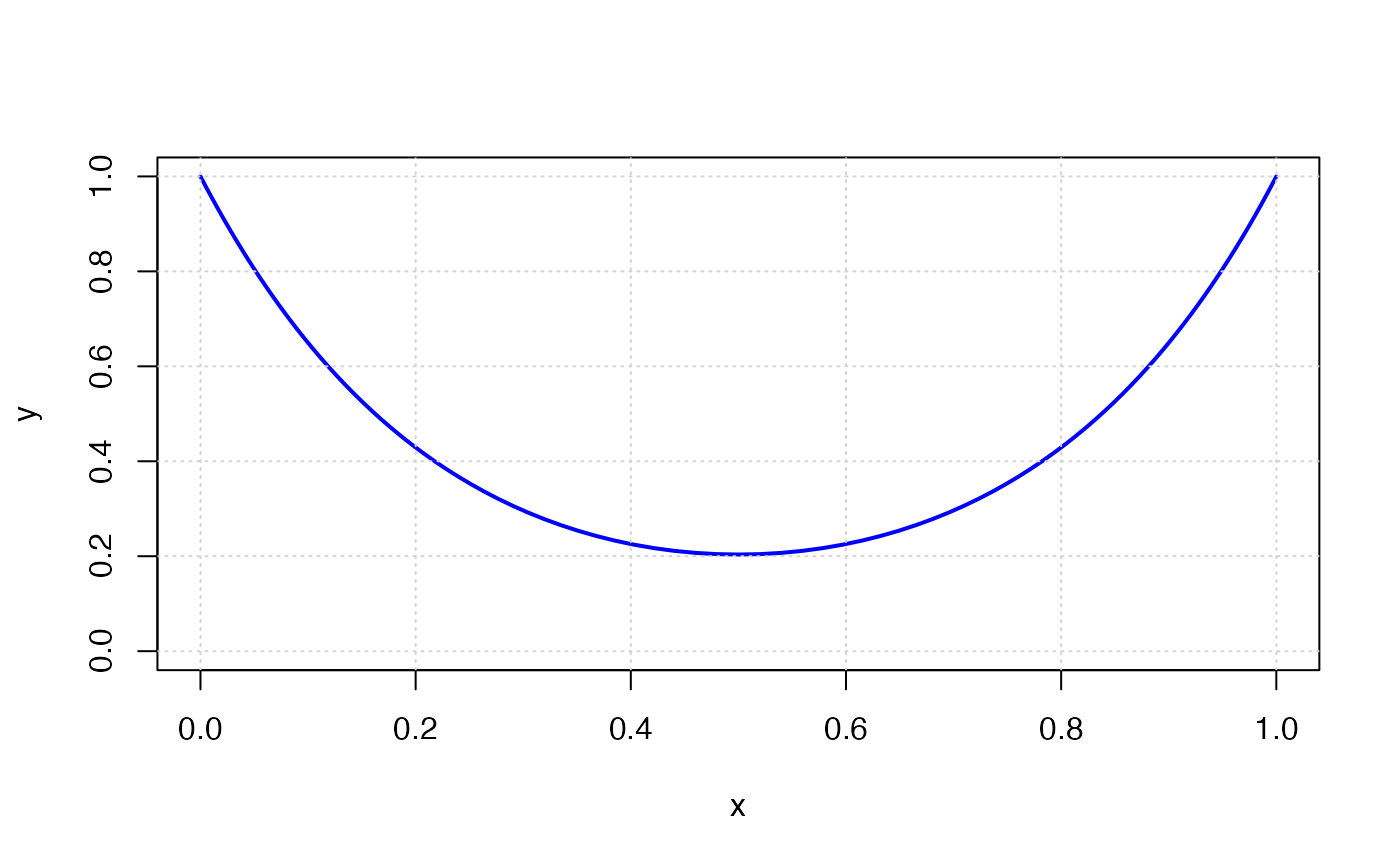
## Plot and compare with ideal catenary
xs <- result$getValue(x)
ys <- result$getValue(y)
plot(c(0, 1), c(0, 1), type = 'n', xlab = "x", ylab = "y")
lines(xs, ys, col = "blue", lwd = 2)
grid()